
|
2. INTERVALS
The Interval is the distance in pitch between two notes, which is given by the number of whole and half steps between them. This number, however, does not indicate the degree of affinity between them nor their relative position in a Major scale. Therefore, it is most common to indicate the interval with a number and a quality. The interval number indicates the number of natural notes between the first and last note, both included. And, unless other thing indicated, it will be assumed that the interval is ascending, that is, that the second note is higher than the first one. Thus, for example, the interval “between D and A” is a 5th (D – E – F – G – A are 5 natural notes in ascending order).
If we now consider the interval “between D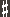 and A and A ”, we find again a 5th (D – E – F – G – A are 5 natural notes in ascending order), although this distance is smaller than that between D and A. To take into account these differences, an interval quality is added to the interval number, which is related to the number of whole and half steps contained in the interval. ”, we find again a 5th (D – E – F – G – A are 5 natural notes in ascending order), although this distance is smaller than that between D and A. To take into account these differences, an interval quality is added to the interval number, which is related to the number of whole and half steps contained in the interval.
The interval quality is based on the Major scale. So, every interval between the lowest C and any other note in the C Major scale in ascending order are called Major (M) or Perfect (P). Particularly, the interval between C and F, G or C is called Perfect, while the interval between C and any other note in this scale is called Major (in Chapter 3 an explanation of it will be given). Table 1 shows these intervals and also indicates the number of whole steps contained in each of them.
Table 1. Intervals in the ascending C Major scale.
| Between C and |
C |
D |
E |
F |
G |
A |
B |
C |
Interval |
P 1st |
M 2nd |
M 3rd |
P 4th |
P 5th |
M 6th |
M 7th |
P 8th |
Number of Whole steps |
0 |
1 |
2 |
2.5 |
3.5 |
4.5 |
5.5 |
6 |
The P 1st interval is called Unison and the P 8th, Octave. To name other different intervals, the following qualities are used:
-
minor (m), if it has one half step less than the corresponding Major interval. For example, between C and E  there is a m 3 rd (1.5 W) and between C and B  there is a m 7 th (5 W).
-
Augmented (A), if it has one half step more than the corresponding Major or Perfect interval. For example, between C and D 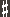 there is an A 2 nd (1.5 W), between C and F 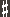 there is an A 4 th (3 W) and between C and A 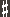 there is a A 6 th (5 W).
-
diminished (d), if it has one half step less than the corresponding minor or Perfect interval. For example, between C and G  there is a d 5 th (3W) and between C and B 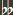 there is a d 7 th (4.5 W).
-
When necessary, the term double Augmented (AA) is used for the interval having one half step more than the Augmented, and the term double diminished (dd) is used for the interval having one half step less than the diminished.
Table 2 shows the intervals between C and the altered notes and also indicates the number of whole steps contained in each of them.
Table 2. Intervals between C and the altered notes.
| Between C and |
C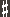 |
D |
D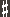 |
E |
F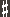 |
G |
G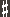 |
A |
A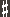 |
B |
Interval |
A 1st |
m 2nd |
A 2nd |
m 3rd |
A 4th |
d 5th |
A 5th |
m 6th |
A 6th |
m 7th |
Number of Whole steps |
0.5 |
0.5 |
1.5 |
1.5 |
3 |
3 |
4 |
4 |
5 |
5 |
The last two rows in Table 1 also serve to determine the interval between any two notes, irrespective of whether the first note is C or not. Let us see some examples:
Those intervals not bigger than an octave, as those studied up to this point, are called simple, while those bigger than an octave are called compound. Every compound interval can be reduced to a simple one by eliminating the proper number of octaves. The interval quality of a compound interval is that of its corresponding simple interval.
|
 |