
|
3. INVERSION OF INTERVALS
The inversion of an interval consists, simply, in interchanging the order of its notes. Thus, if we invert the interval D – A, which is a P 5th, we obtain the interval A – D, which is a P 4th. And, if we invert the interval E – G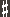 , which is a M 3rd, we obtain the interval G , which is a M 3rd, we obtain the interval G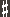 – E, which is a m 6th. In the inversion of intervals, the following two rules apply: – E, which is a m 6th. In the inversion of intervals, the following two rules apply:
- The sum of the interval numbers of a given interval and its inversion is always 9.
-
When inverting intervals, the Major is transformed into minor, the minor into Major, the Augmented into diminished, the diminished into Augmented, the double Augmented into double diminished and the double diminished into double Augmented. The Perfect interval, however, remains Perfect.
We can check these two rules in the two previous examples. So, in the first one, the P 5th becomes a P 4th (5 + 4 = 9 and both of them are P); and, in the second one, the M 3rd becomes a m 6th (3 + 6 = 9 and M becomes m).
In practice, the inversion of an interval is achieved by raising the lower note one octave or by lowering the higher note one octave. But the same result is reached by changing the ascending character of the interval to descending. Thus, between D and A there are 5 natural notes in ascending order (D – E – F – G – A) and a distance of 3.5 W, so it is a P 5th. But, in descending order, there are 4 natural notes (D – C – B – A) and a distance of 2.5 W, that is, a P 4th. Therefore, the inversion of the interval can be understood in these two different ways.
It is very illustrative to verify that, in the descending C Major scale, every interval between the highest C and any other note in the scale is minor or Perfect. Table 3 shows these intervals and also indicates the number of whole steps contained in each of them.
Table 3. Intervals in the descending C Major scale.
| Between C and |
C |
B |
A |
G |
F |
E |
D |
C |
Interval |
P 1st |
m 2nd |
m 3rd |
P 4th |
P 5th |
m 6th |
m 7th |
P 8th |
Number of Whole steps |
0 |
0.5 |
1.5 |
2.5 |
3.5 |
4 |
5 |
6 |
If we compare Table 3 with Table 1 in Chapter 2, we will see that, apart from the 1st and 8th intervals, only the 4th and 5th have the same number of whole and half steps in both the ascending and the descending scale. On the other hand, notes F and G are very affine to note C, due to the particular relationships among their frequencies, from the physical point of view. As a consequence of all these things, these intervals are called “Perfect”. Remember that the P 4th and the P 5th are the inversion of each other.
Although to a smaller extent, those notes forming M 3rd or m 3rd intervals with C are also very affine to it, as well as their corresponding inversions, the m 6th and M 6th, respectively. This concept of affinity several times mentioned is technically known as Consonance and is related to the physical phenomenon of vibration, which originates the sound. In summary, we can say that, apart from the unison and the octave, the Consonant intervals are the P 5th, the M 3rd and the m 3rd, along with their inversions, the P 4th, the m 6th and the M 6th, respectively. The rest of the intervals are Dissonant. In practice, this means that if two notes forming a consonant interval are simultaneously heard, a sensation of harmony, rest and stability is perceived. On the contrary, hearing at the same time two notes forming a dissonant interval produces a sensation of tension and instability.
Finally, in Tables 1 and 3 we can also observe that all possible interval distances appear, except the 3 W or Tritone, a highly dissonant interval having special properties. Actually, with the notes of the C Major scale it is possible to form only one tritone, the F – B (A 4th) or its inversion B – F (d 5th).
The concept of Octave and its division in 12 parts, the concept of Consonance and the concept of Major scale are 3 fundamental principles which the Western Music is based on, irrespective of the musical style considered.
|
 |